Sheep Sparks
搜索
关于

计算流体力学入门（一）

|
访问
本文共1,093字。

流体力学的概念、物质导数及速度散度

1. 计算流体力学到底是什么？

从物理的角度来分析，任何流体的流动均遵守三大基本定律：

  • 质量守恒

  • 牛顿第二定律

  • 能量守恒

这三大基本定律能够用数学方程的形式表达，最基本的形式可以是积分方程，也可以是偏微分方程。计算流体力学是将这些积分型或偏微分型方程转换成离散代数形式，然后求解这些代数方程以得到离散的空间和时间点上的流场数值。

2. 三大基本控制方程简介

控制方程有不同的表达形式，方程的特定形式对大多数空气动力学理论几乎没有什么不同，然而，对于CFD中的某一算法，使用某种形式的控制方程可以得到成功的结果，而使用另一形式的控制方程就有可能导致数值结果的震荡、得到不正确的结果，甚至数值失稳。因此在CFD世界中，方程的形式是至关重要的。

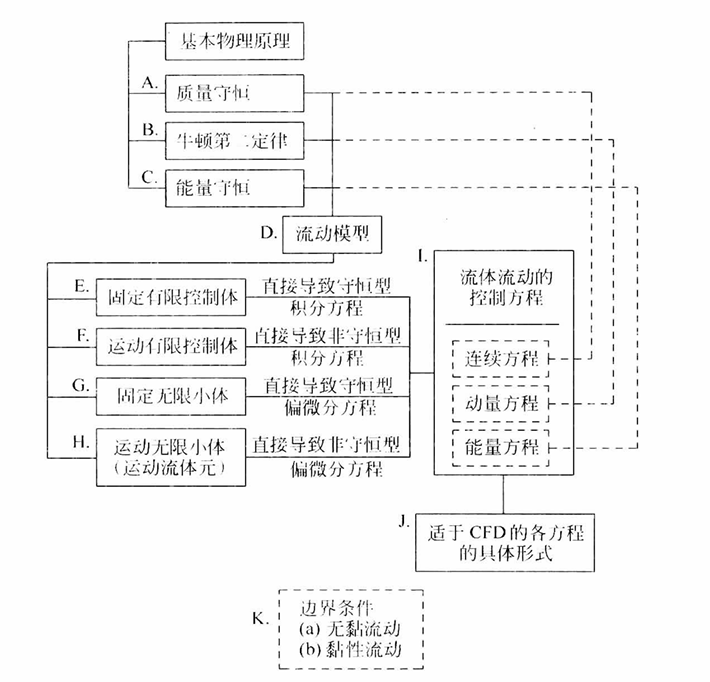
2.1 流动模型

对于运动中的流体，不同的位置可以有不同的速度。我们如何将运动的流体可视化，以将基本的物理原理应用于其中呢？对于连续流体，答案是构造下述的四个模型之一：

2.1.1 有限控制体

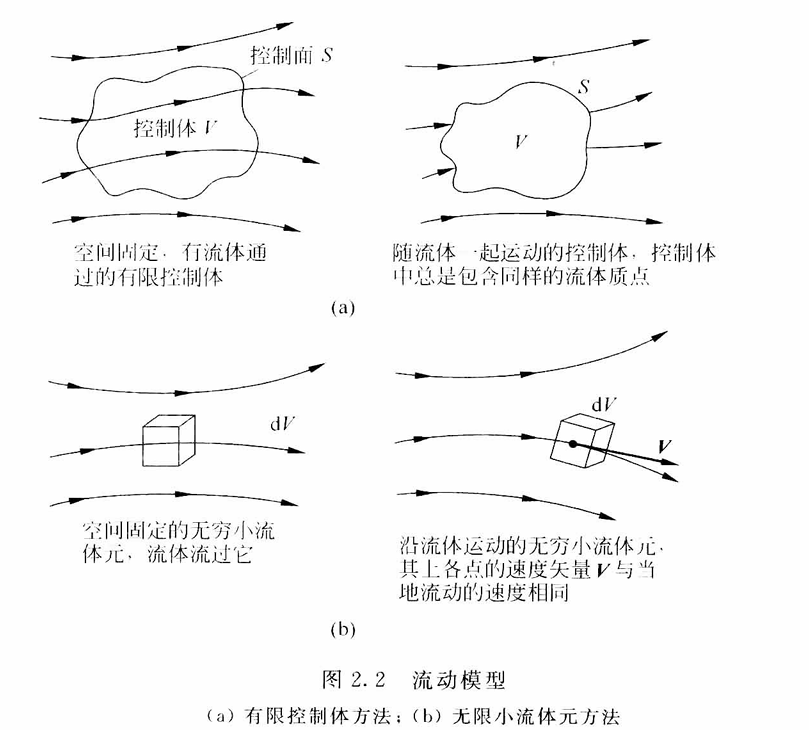
将基本物理原理应用于有限控制体，可以直接得到流体流动方程，它们是积分型的。处理这些积分型控制方程，从而间接得到偏微分方程。由空间固定的有限控制体得到的方程，不管是积分型的还是偏微分型的，都是守恒型控制方程。由随流体运动的有限控制体得到的方程，不管是积分型的还是偏微分型的，都是非守恒型控制方程。

2.1.2 无穷小流体元

我们将基本物理原理仅仅应用于无穷小流体元本身，这一应用将直接导致偏微分形式的基本方程。由空间固定的流体元直接得到的偏微分方程是守恒型方程，由运动流体元直接得到的偏微分方程依然是非守恒型方程。

2.1.3 一些注释

现阶段只要意识到存在两种不同形式的方程就足够了。

2.2 物质导数（随运动流体元的时间变化率）

对于密度场ρ=ρ(x,y,z,t)\rho = \rho(x,y,z,t)，对其在流场中某一点进行泰勒展开：

ρ2=ρ1+(∂ρ∂x)1(x2−x1)+(∂ρ∂y)1(y2−y1)+(∂ρ∂z)1(z2−z1)+(∂ρ∂t)1(t2−t1)+(高阶项)\begin{aligned} \rho_{2}= & \rho_{1}+\left(\frac{\partial\rho}{\partial x}\right)_{1}(x_{2}-x_{1})+\left(\frac{\partial\rho}{\partial y}\right)_{1}(y_{2}-y_{1})+\left(\frac{\partial\rho}{\partial z}\right)_{1}(z_{2}-z_{1}) \\ & +\left(\frac{\partial\rho}{\partial t}\right)_1(t_2-t_1)\quad+(\text{高阶项}) \end{aligned}

两端同时除以t2−t1t_2-t_1，忽略高阶小量，得到：

ρ2−ρ1t2−t1=(∂ρ∂x)1x2−x1t2−t1+(∂ρ∂y)1y2−y1t2−t1+(∂ρ∂z)1z2−z1t2−t1+(∂ρ∂t)1\frac{\rho_2-\rho_1}{t_2-t_1}=\left(\frac{\partial\rho}{\partial x}\right)_1\frac{x_2-x_1}{t_2-t_1}+\left(\frac{\partial\rho}{\partial y}\right)_1\frac{y_2-y_1}{t_2-t_1}+\left(\frac{\partial\rho}{\partial z}\right)_1\frac{z_2-z_1}{t_2-t_1}+\left(\frac{\partial\rho}{\partial t}\right)_1

将物质导数定义为

lim⁡t2→t1ρ2−ρ1t2−t1≡DρDt\lim_{t_2\to t_1}\frac{\rho_2-\rho_1}{t_2-t_1}\equiv\frac{\mathrm{D}\rho}{\mathrm{D}t}

上式代表当流体元经过1点时密度随时间的瞬时变化率。物质导数是针对特定流体元的，与∂ρ∂t\frac{\partial\rho}{\partial t}不同，后者是针对流场中固定的一点的。

2.3 速度的散度及其物理意义

速度的散度∇⋅V\nabla\cdot V的物理意义是随流体一起运动的控制体体积随时间的相对变化率。

共0条搜索结果。